Kreativita není jen o talentu či intuici, ale i o exaktních pojmech. Jedním takovým je zlatý řez – častý poměr proporcionality objektů objevující se jak v přírodě, tak i v umělecké tvorbě. Praktické uplatnění však dlouhodobě nachází i v designu.

Řecké písmeno „fí“ (v řecké abecedě psané velkým Φ a malým φ) v matematice popisuje jedno velmi zajímavé iracionální číslo. Je odvozeno od přibližného výsledku geometrické úlohy, která zní: rozdělit úsečku na dvě části tak, aby poměr delší části ke kratší části byl stejný jako poměr délky celé úsečky k delší části. Tedy, pokud x je délka úsečky, a je její delší část a b je její kratší část, musí platit a/b = x/a, čili:
a/b = (a+b)/a
Tento vztah má po zjednodušení na kvadratickou rovnici dva výsledky (kořeny) a jedním z nich je číslo s přibližnou hodnotou 1,618033, nazývané také „zlatý řez“, či „zlatý podíl“ (lat. sectio divina).
Proč zlatý? Ukázalo se, že proporcionalita v poměrech blízkých fí se nezřídka vyskytuje nejen v obdivuhodných přírodních strukturách, ale je typická i pro mnohé lidské umělecké výtvory, často považované za esteticky hodnotné, ne-li přímo klasická díla. Domněnky některých vědců dokonce sahají až tak daleko, že naznačují spojitosti mezi zlatým poměrem a jakýmsi vrozeným smyslem pro krásu.

Historie
Kdy přesně bylo fí objeveno, není známo. Za své označení vděčí řeckému sochaři a matematikovi jménem Feidiás (Phidias, 5. století př. n. l.), který tento oku lahodící poměr používal při tvorbě svých soch. Analýza rozměrů egyptských pyramid však naznačuje, že zlatý řez byl pravděpodobně prakticky využíván již při jejich stavbě v třetím tisíciletí př. n. l.
Fí bylo ve středověku hojně používáno při kalkulacích spojených s pravidelnými pětiúhelníky a pentagramy jak na evropském kontinentu, tak i v arabském světě. V roce 1202 se na území nynější Itálie objevil manuskript Liber Abaci (Kniha výpočtů) a jeho autorem byl matematik Leonardo z Pisy, posmrtně známý pod jménem Fibonacci. Snad nejpamátnější sekce manuskriptu pojednává o hypotetické populaci králíků, množící se měsíčně podle systematických pravidel. Aby Fibonacci vypočítal, kolik králíků bude mít populace po období jednoho roku, popsal číselnou řadu, která začíná čísly 0 a 1. Každý další člen řady přibývá tak, že se sčítají dva předešlé členy, tedy: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... Čísla Fibonacciho sekvence mají mnoho neobyčejných charakteristik a jednou z nich je, že při dělení dvou sousedících čísel (většího menším) je výsledek vždy velmi blízký fí. Tento fakt zřejmě samotnému Fibonaccimu unikl, ale postupně si ho všimlo několik slavných matematiků, kromě jiných Edouard Lucas (ten řadu pojmenoval po Fibonaccim) i Johannes Kepler. Lucas také od Fibonacciho řady odvodil podobnou řadu (2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, ...), ve které je podíl sousedících také fí.
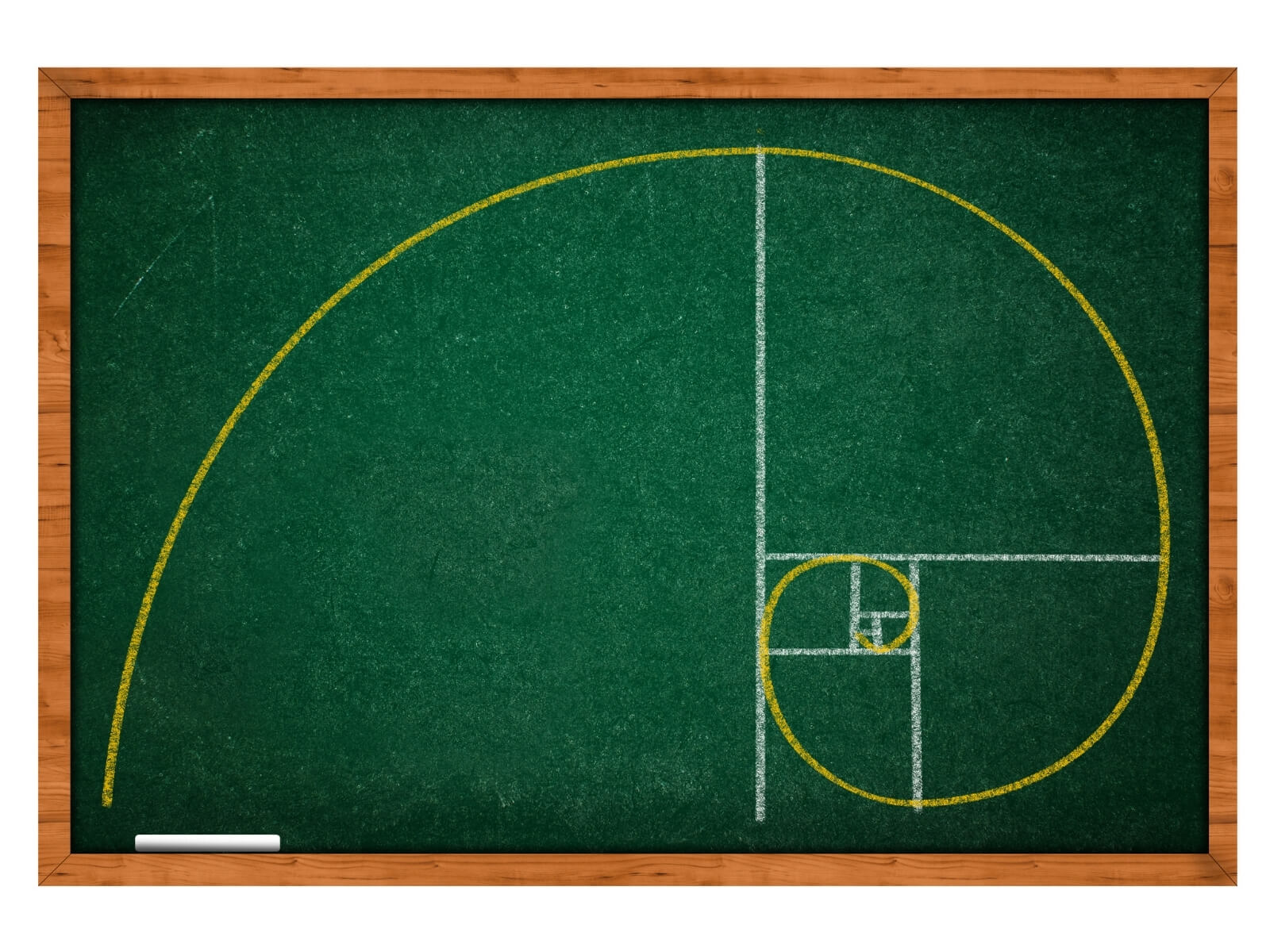
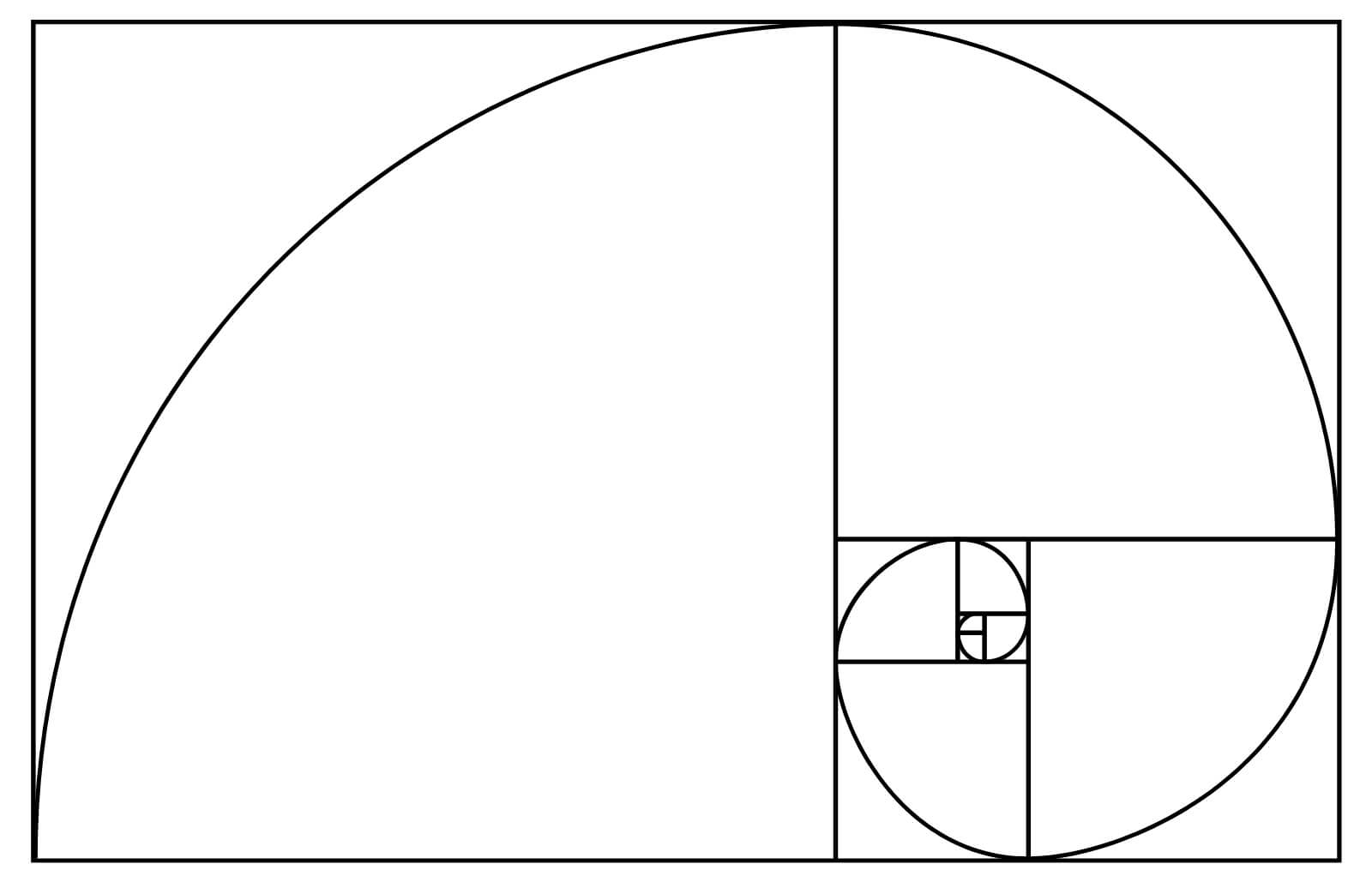
Když se čísla Fibonacciho řady umocní na druhou, vzniknou čtverce. Tyto čtverce je následně možné uložit způsobem, aby se navzájem doplňovaly tak, že budou plošnou demonstrací zlatého řezu. V každém ze čtverců je také možné narýsovat přesný oblouk spojující dva protilehlé vrcholy. Jeho poloměr je příslušné Fibonacciho číslo a střed má v jednom z vrcholů příslušného čtverce. A pokud jsou oblouky narýsované tak, že každý začíná v bodě, kde končí ten předchozí (z pohledu pořadí čtverců podle Fibonacciho řady) vznikne tvar spirály – „zlaté spirály“.
Fascinace zlatým řezem a Fibonacciho řadou pokračuje dodnes, známé jsou například takzvané Penroseovy aperiodické obklady, díla moderního holandského malíře Pieta Mondriana, či architektura Le Corbusiera.

Příklady zlatého řezu (a Fibonacciho sekvence)
Říše přírody nabízí mnoho úžasných a nečekaných příkladů pro utvoření si konkrétnější představy o abstraktních matematických konceptech zlatého řezu a Fibonacciho řady.
- Počet lupenů květů je velmi často identický s některým z čísel Fibonacciho řady a i při druzích, které tvoří výjimku (jako fuchsie) je počet lupenů členem Lucasova radu.

- Uspořádání semen koncentrovaných uprostřed květu slunečnice nebo echinacey vykazuje tvar zlaté spirály.

- Struktura šišek borovice při pohledu zespodu také odhaluje uspořádání jednotlivých segmentů ve tvaru známé spirály.

- Jinak tomu není ani u hlávek květáku či brokolice odrůdy romanesco.

- Fibonacciho číselnou sekvenci je možné sledovat i u uspořádání listů rostlin na stopce a zdá se být optimálním řešením polohy listů tak, aby si navzájem nestínily. Podobně také při rozvětvování stromů na úrovních směrem od kmene nahoru často přibývají větve tak, že celkové počty jsou 2, 3, 5, 8, 13, atd.
- Mušle šneků a mořských živočichů jsou dalším z řady příkladů zlaté spirály.

- I tvary hurikánů na záběrech z družice a spirálních galaxií pořízených pomocí teleskopu dokumentují výskyt téhož vzoru, tentokrát v anorganické formě.
- Proporcionalita lidské tváře, funkčních částí těl živočichů, poměr počtu samiček a samečků v koloniích hmyzu, stavba některých vnitřních orgánů, či dokonce struktura DNA – všechny z těchto organických celků vykazují větší, či menší spojitost se zlatým poměrem fí.
Jednoduchost a krásu rozložení objektu na menší části v poměru přibližně 1,618 není problém vystopovat ani v dílech malířů, sochařů a architektů. V Botticelliho obraze Zrození Venuše je takto znázorněno tělo bohyně, Michelangelo ve Stvoření Adama zvolil zlatý poměr mezi částmi obrazu definovanými hlavním postavám scény a v Seuratově mistrovském díle Koupání v Asnieres jsou takto důmyslně rozloženy všechny sekce malby. Da Vinciho i Dalího zpracování námětu poslední večeře, portréty Mony Lisy, Dámy s hranostajem i Dívky s perlovou náušnicí, či moderní abstraktní díla Mondriana následují stejný kompoziční princip.

I antický ideál krásy zhmotněný v sochách postav lidí i bohů na mnoha příkladech dokladuje zlatý poměr – tentokrát dolní části lidského těla k horní, s dělicí linií přesně ve výši pupku, který je díky obnažení postav často viditelný.
Aplikace zlatého řezu na architektonické prvky světoznámých budov má, i díky již zmíněným egyptským pyramidám, za sebou snad nejdelší historii. Architekti se tomuto poměru nevyhýbali v žádném období a jeho přítomnost je tak patrná v typických stavbách téměř každého ze slohů – Parthenón, Taj Mahal, Notre-Dame, Villa Stein jsou jen několika z mnoha.

Zlatý řez v designu
Současný přístup ke kompozici v designu se neřídí žádnými pevně danými pravidly. Ani zlatý řez není samozřejmou zárukou atraktivity, ale jako inspirace pro určité fundamentální praktiky při rozvrhování hrubé struktury návrhu, mřížky v pozadí, hierarchie prvků a podobně může skvěle posloužit. Všechno jsou to věci, které designér nikdy nenavrhuje s cílem, aby si jich všiml konečný uživatel, či spotřebitel. Zlatý poměr má tvořit neviditelný organizační princip, který je spíše pociťován než vnímán rozumem.
Jedním dobrým orientačním faktorem je celková velikost designovaného objektu – čím je větší (nábytek, billboard), tím více záleží i na detailech kompozice.

Způsobů, jak uvedené zásady implementovat v praxi, je několik. Uspořádání prvků a výpočet jejich přesných dimenzí lze realizovat tak, aby výsledné poměry hlavních rozměrů byly přibližně rovné fí. Uplatnění se jistě osvědčí ve webdesignu u dvousloupcového zobrazení hlavního obsahu a bočního panelu menu, ale koncepce zobrazení elementů v rámci těchto celků může být identická.
Plošný sled čtverců čísel Fibonacciho řady může být zase vhodným pokynem pro dodržení intervalů volného místa („whitespace“) s cílem zachování lepší přehlednosti a čitelnosti obsahu.
Trasování zlaté spirály jako hlavního proudu obsahu, přirozeně navádějícího zrak směrem do jejího centra, má potenciál zachytit a upoutat pozornost nenásilným způsobem. Pokud jsou všechny klíčové prvky umístěny u linie spontánního víru spirály, je těžké si jich nevšimnout. Přirozeně, obsah směrem do centra houstne, proto je důležité myslet i na srozumitelnost, barevné schéma a podobně.
„Pravidlo třetin“ je aplikovatelné při rozvrhování kombinace obrázků a textu, obvykle titulku. Využívá druhý z kořenů řešení kvadratické rovnice zlatého řezu, kterým je 0,618033. Rozdělení designu na tři sekce v poměru 1:0,618:1 vertikální a tři sekce v témže poměru horizontální vytvoří mřížku a v místech, kde se její pomyslné dělící linie protínají, je vhodné umístit prvky, na které se klade důraz.
„Zlaté kružnice“, čili kružnice s průměrem čísel Fibonacciho řady, jsou uplatnitelné při grafické přípravě loga na dosažení harmonie mezi různými tvary, hranatými i oblejšími. Velmi pěkné výtvory mohou vzniknout i kreativním spojováním takových kružnic do nových soustav, jejich vzájemným překládáním a prolínáním.


 CZ
CZ 
